機械制圖投影知識介紹

今天來給大家介紹下浩辰CAD機械制圖中的投影知識，希望能夠給大家帶來幫助。

一、投影法的基本知識

1 ．投影的形成原理。

用光線照射物體，在預設的面上繪制出被投射物體圖形的方法，叫做投影法。光線叫做投射線，所投射的面叫做投影面，投影面上等到的物體圖形叫做該物體的投影。

2 ． 投影法種類

中心投影法： 投射線都從投影中心出發，在投影面上作出物體圖形的方法叫做中心投影法。

平行投影法： 若將投射中心移至無窮遠處，則所有的投射線就相互平行。用相互平行的投射線，在投影面上作出物體圖形的方法叫做平行投影法。在平行投影法中，根據投影面是否垂直于投影面，又分為兩種：

斜投影　投射線傾斜于投影面

正投影　投射線平行于投影面

正投影法能準確地表達出物體的形狀結構，而且度量性好，因而在工程上廣泛應用。但它的缺點是立體感差，一般要用兩個或兩個以上的圖形才能把物體的形狀表達清楚。機械圖形主要是用正投影法繪制的，所以正投影法是本課程學習的主要內容。在以后的課程中，除有特別說明外，我們提到的投影均指正投影

3 ．正投影法的投影特性，以直線、平面相對于投影面位置的不同，講明實形性、積聚性和類似性三大主要特性。

二、物體三視圖的形成及投影規律

1、三視圖的形成

用三個互相垂直的投影面構成一空間投影體系，即正面V、水平面H、側面W，把物體放在空間的某一位置固定不動，分別向三個投影面上對物體進行投影，在V面上得到的投影叫做主視圖，在H面上得到的投影叫俯視圖，在W面上得到的投影叫左視圖。為了在同一張圖紙上畫出物體的三個視圖，國家標準規定了其展開方法：V面不動，H面繞OX軸向下旋轉90°與V面重合，W面繞OZ軸向后旋轉90°與V面重合，這樣，便把三個互相垂直的投影面展平在同一張圖紙上了。三視圖的配置為：以主視圖為基準，俯視圖在主視圖的下方；左視圖在主視圖的右方。

2、視圖之間的投影規律

每個視圖反映物體兩個方向的尺寸。主視圖反映物體的長度和高度；左視圖反映寬度和高度；俯視圖反映長度和寬度。按照三視圖的配置，三視圖的投影規律為：長對正，高齊平，寬一致。

三視圖的投影規律是在畫圖、看圖時都須嚴格遵守的。

3、視圖中圖紙及線框的含義

在繪制物體的三視圖時，物體表面上的線、面與視圖中的輪廓線、線框都有著一一對應的關系。

（1）、視圖中每一條輪廓線的含義

物體表面上交線的投影；物體上垂直于投影面的平面或曲面的投影；面立體轉向輪廓線的投影。

（2）、視圖中每一封閉線框的含義：

視圖中每一個封閉線框都表示物體上的一個面（平面或曲面）的投影。

視圖中圖線及線框的含義是畫圖、看圖的依據，并可根據其含義對視圖的正確性進行檢查。

（ 3）、物體的空間方位

物體有上、下、左、右、前、后、六個方向的位置關系，每個視圖能反映物體的四個方位。主視圖反映物體的上、下、左、右，左視圖反映物體的上、下、前、后，俯視圖反映物體的前、后、左、右。根據以上位置關系，可以在各視圖上分析出物體各部分的空間位置，以便增強對物體的空間想象能力。

三、三視圖的畫圖步驟

根據物體或立體圖畫三視圖時，應把物體擺平放正，選擇形體主要特征明顯的方向作為主視圖的投影方向，一般畫圖步驟如下：

1、用點畫線和細實線畫出各視圖的作圖基準線。

2、用細實線、虛線，按照物體的構成，先大后小，先整體，后局部的順序，用三視圖的投影規律，畫出物體三視圖的底圖。

3、底圖畫完后，需經過檢查，沒有錯誤后并清理圖面，再按圖線要求描深。圖線的描深順序為：先曲線，后直線；水平線應自上而下，依次描深，垂線應自左向右依次描深。按照這種順序描深，可以保證曲線與直線的正確連接，提高描深速度，保證圖面的清潔。

CAD教程第5章-機械制圖投影知識(2)

時間：2011-07-14 19:44:11   作者：未知   來源：網絡轉載   閱讀：984   評論：0

點的投影

一、點在兩個投影面體系中的投影

如圖

點在兩面體系中的投影

投影特性：

（ 1 ）點的正面投影和水平投影連線垂直 OX 軸，即 a’a ⊥ OX;

（ 2 ）點的正面投影到 OX 軸的距離，反映該點到 H 面的距離，點的水平投影到 OX 軸的距離，反映該點到 V 面的距離，即 a’ax=Aa, aax=Aa’ 。

二、點在三個投影面體系中的投影

點在兩面投影體系已能確定該點的空間位置，但為了更清楚地表達某些形體，有時需要在兩投影面體系基礎上，再增加一個與 H 面及 V 面垂直的側立的投影面 W 面，形成三面投影體系。如下圖。

點在三面體系中的投影

投影特性：（ 1 ） a’a ⊥ OX, a’a” ⊥ OZ, aayH ⊥ OYH, a”ayW ⊥ OYW

（ 2 ） a’ax=Aa, aax=Aa’ 。 a’aZ=Aa”

三、點的投影與坐標

根據點的三面投影可以確定點在空間位置，點在空間的位置也可以由直角坐標值來確定。

點的正面投影由點的 X 、 Z 坐標決定，點的水平投影由點的 X 、 Y 坐標決定，點的側面投影由點的 Y 、 Z 坐標決定。

例題 1 已知點 A （ 20 ， 15 ， 10 ）、 B （ 30 ， 10 ， 0 ）、 C （ 15 ， 0 ， 0 ）求作各點的三面投影。

分析：由于 ZB=0 ，所以 B 點在 H 面上， YC=0 ， ZC=0 ，則點 C 在 X 軸上。

在 OX 軸上量取 oax=20;

過 ax 作 aa’ ⊥ OX 軸，并使 aax=15, a’aZ=10;

過 a’ 作 aa” ⊥ OZ 軸，并使 a”aZ= aax, a, a’,a” 即為所求 A 點的三面投影。

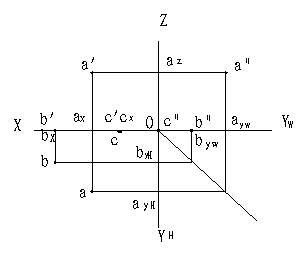
根據點的坐標求點的投影

作 B 點的投影：

在 OX 軸上量取 obX=30;

過 bX 作 bb’ ⊥ OX 軸，并使 b’bX=0, bbX=10, 由于 ZB=0 ， b’,bX 重合。即 b’ 在 X 軸上；

因為 ZB=0 ， b’ 在 OYW 軸上，在該軸上量取 Obyw=10, 得 b” ，則 b 、 b’ 、 b” 即為所求 B 點的三面投影。

作 C點的投影 ：

由在 OX 軸上量取 OCX=15;

于 Yc=0 ， Zc=0,c 、 c’ 都在 OX 軸上，與 c 重合， c” 與原點 O 重合。

四、兩點的置點相對在同面投影的位坐標來判斷，其中左右由 X 坐標差判別，上下由 Z 坐標差判別

空間點的相對位置，可以利用兩，前后由 Y 坐標差判別。如圖。

兩點間的相對位置

Za>ZbA 點在 B 點上方， Ya>YbA 點在 B 點的前方， Xa>XbA 點在 B 點的左方。 A 點在 B 點的左前上方。

5 、重影點

當空間兩點位于垂直于某個投影面的同一投影線上時，兩點在該投影面上的投影重合，稱為重影點。 [yao_page]

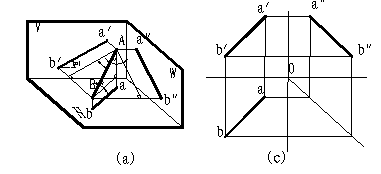
直線的投影

直線可以由線上的兩點確定，所以直線的投影就是點的投影，然后將點的同面投影連接，即為直線的投影，如圖。

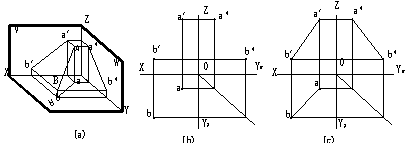
直線的三面投影

一、各種位置直線的投影

（ 1 ）投影面平行線

直線平行于一個投影面與另外兩個投影面傾斜時，稱為投影面平行線。

正平線——平行于 V 面傾斜于 H 、 W 面；

水平線——平行于 H 面傾斜于 V 、 W 面；

側平線——平行于 W 面傾斜于 H 、 V 面。

投影面平行線特性：

平行于那個投影面，在那個投影面上的投影反映該直線的實長，而且投影與投影軸的夾角，也反映了該直線對另兩個投影面的夾角，而另外兩個投影都是類似形，比實長要短。

CAD教程第5章-機械制圖投影知識(3)

時間：2011-07-14 19:44:11   作者：未知   來源：網絡轉載   閱讀：986   評論：0

（ 2 ）投影面垂直線

直線垂直于一個投影面與另外兩個投影面平行時，稱為投影面垂直線。

正垂線——垂直于 V 面平行于 H 、 W 面；

鉛垂線——垂直于 H 面平行于 V 、 W 面；

側垂線——垂直于 W 面平行于 V 、 H 面。

投影面垂直線特性：

垂直于那個投影面，在那個投影面上的投影積聚成一個點，而另外兩個投影面上的投影平行于投影軸且反映實長。

（ 3 ）一般位置直線

直線與三個投影面都處于傾斜位置，稱為一般位置直線。

一般位置直線

一般位置直線在三個投影面上的投影都不反映實長，而且于投影軸的夾角也不反映空間直線對投影面的夾角。

二、一般位置直線的實長及其與投影面夾角

一般位置直線的投影即不反映實長又不反映對投影面的真實傾斜角度。要求得實長和夾角，我們利用直角三角形法求得。如圖所示。

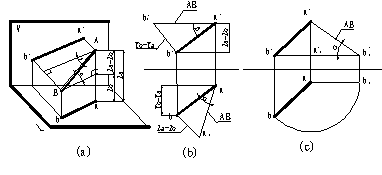
求一般位置直線的實長及對投影面的夾角

三、 直線上點的投影

如果點在直線上，則點的各個投影必在該直線的同面投影上，并將直線的各個投影分割成和空間相同的比例。

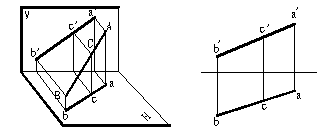
直線上的點

四、兩直線的相對位置

（ 1 ） 兩直線平行

兩直線平行

兩直線空間平行，投影面上的投影也相互平行。

（ 2 ）兩直線相交

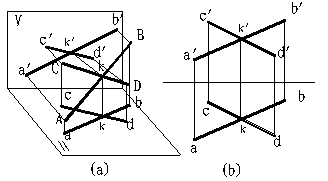
兩直線相交

空間兩直線相交，交點 K 是兩直線的共有點， K 點的投影，符合點的投影規律。

（ 3 ）兩直線交叉

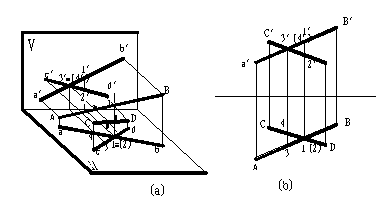
兩直線交叉

空間兩直線不平行又不相交時稱為交叉。交叉兩直線的同面投影可能相交，但它們各個投影的交點不符合點的投影規律。

五、兩直線垂直相交

空間兩直線垂直相交，其中有一直線平行于某投影面時，則兩直線在所平行的投影面上的投影反映直角。

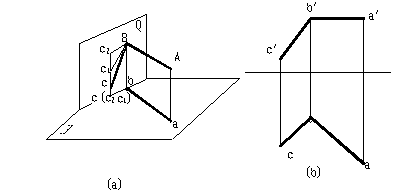
垂直相交兩直線的投影

證明：因為 AB ⊥ BC ， AB ⊥ Bb ，所以 AB 必垂直于 BC 和 Bb 決定的平面 Q 及 Q 面上過垂足 B 的任何一直線（ BC1 、 BC2…… ）因 AB ∥ ab 故 ab 也必垂直于 Q 面過垂足 b 的任一直線，即 ab ⊥ bc 。

例題：如圖，已知點 C 及直線 AB 的兩面投影，試過 C 點作直線 AB 的垂線 CD ， D 為垂足，并求 CD 的實長。

求點到直線的垂足及距離

分析：因為 ab ∥ OX ，所以 AB 是正平線，又因 CD 與 AB 垂直相交， D 為交點，則 a’b’ ⊥ c’d’, 由 d’ 可在 ab 上求得 d 。利用直價三角形法可求得 CD 的實長。

作法： 1 ） c’ 作 c’d’ ⊥ a’b’ 得交點 d’ ；

2 ）由 d’ 引投影連線與 ab 交得 d;

3 ）連 c 和 d ，則 c’d’ 、 cd 即為垂線 CD 的兩面投影；

4 ）用直角三角形法求得 C 與直線 AB 之間的真實距離 CD 。

以上就是機械制圖投影知識的介紹，大家感興趣的可以動手試試吧！