CAD繪圖技巧之阿波羅尼斯圓(阿氏圓)

我們在使用浩辰CAD軟件繪制CAD圖形文件的時候，會聽到有人說要繪制阿氏圓也就是阿波羅尼斯圓，今天的CAD繪圖技巧小編就來給大家介紹一下。

什么是阿波羅尼斯圓(阿氏圓)？
阿波羅尼斯（Apollonius）圓在平面上給定相異兩點A、B，設P點在同一平面上且滿足PA/PB= λ， 當λ>0且λ≠1時，P點的軌跡是個圓，這個圓我們稱作阿波羅尼斯圓。

如圖PA=PB=0.5

當λ=1是，軌跡為直線AB的中垂線。

如圖：

阿波羅尼斯圓(阿氏圓)的軌跡圓應該如何做呢？

根據三點確定一個圓這個最簡單的定理，我們只要能找到這個圓上的三點，那么就可以根據這三點作出這個軌跡圓（也就是阿氏圓了），假設這個比為1:2，那么過程如下divide命令把AB平分為3份，那么AP/BP=1:2 過A點做一半徑為X的圓，過B點做一半徑為2X的圓，X任意，確保兩圓能相交就可以了（黃色的兩個圓）用三點作圓（一點為靠近A的平分點，另外兩點為上面兩個黃色圓的交點），得到青色的圓就是我們所求的軌跡圓。

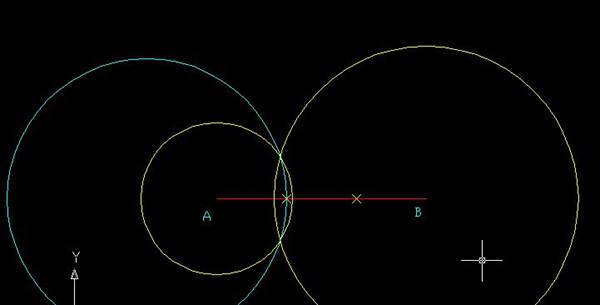
其實實質就是：

點P的軌跡，是以定比m：n內分和外分定線段的兩個分點的連線為直徑的圓什么為內點與外分點呢？見下圖：

我們可以通過公式推導出AN的長度

AN/BN == AP/BP 其中BN=AN+AB

所以

AN/(AN+AB) == AP/BP

===>

AN=AP*AB/(BP-AP)

以NP為直徑的圓就是我們所求的軌跡圓

通過以上的CAD繪圖技巧介紹，相信大家對阿波羅尼斯圓(阿氏圓)也有了一定的認識，之后有人說到阿波羅尼斯圓(阿氏圓)我們也就不再陌生了。